Algoritmo alternativo para divisão de frações

Em um post anterior, explicamos a razão por detrás do algoritmo mais conhecido para dividir frações (“manter a primeira e multiplicar pelo inverso da segunda”), além de discutir brevemente os significados da divisão que podem surgir nesse tipo de operação. Então, assunto esgotado? De modo algum! Mesmo uma simples operação guarda uma ampla gama de possibilidades algorítmicas, desafiando a ideia de que a matemática seja uma ciência estanque, feita, sobretudo, de regras e procedimentos prontos.

Vamos lá!

Imagine que você é um professor de matemática e um dos seus alunos, digamos Rafael, realiza a divisão de 12/15 por 3/5 da seguinte forma:

Solução do Rafael

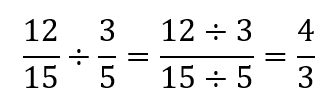
Como você avaliaria a resposta do Rafael? Tire um tempinho para pensar antes de seguir com a leitura!

Em primeiro lugar, precisamos decidir se o que Rafael fez está correto ou não. Podemos notar que ele não usou o algoritmo usual. Se tivesse usado, o resultado seria:

Solução pelo algoritmo tradicional

Opa! Rafael chegou ao resultado correto!

Mas será que isso basta? Ele pode ter dado sorte, apesar de ter partido de um procedimento equivocado?

Vamos analisar seu procedimento. O que ele fez? Ele dividiu os numeradores entre si e também os denominadores, encontrando, respectivamente, o numerador e o denominador do resultado da divisão.  Vamos testar esse procedimento para uma divisão envolvendo outras frações:

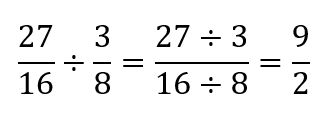
          Você pode verificar facilmente que esse resultado também está correto.

Os pesquisadores Gabriela Gibim, Laura Rifo, Nuria Climent e Miguel Ribeiro conduziram uma pesquisa, durante uma formação docente, em que expuseram os professores a produções de estudantes que se utilizavam de diferentes procedimentos para dividir frações. Então, perguntaram aos professores se as produções estavam corretas ou não e porquê.

Vamos comentar algumas das respostas dos professores acerca do procedimento usado pelo nosso hipotético aluno Rafael.

Fonte: Gibim et al. Conhecimento interpretativo de professores em uma tarefa de divisão de frações. PNA, 19 (3), p. 305-329, 2025.

Pode-se observar que existe uma desconfiança, por parte dos professores, de que esse procedimento não valha sempre. Inclusive, uma das professoras comenta que parece valer apenas quando numeradores e denominadores são múltiplos entre si. De fato, quando eles são múltiplos entre si, isso torna o procedimento do Rafael mais fácil de executar, nos permitindo, portanto, testar diversos casos.

Mas o que ocorre quando os numeradores e os denominadores não são múltiplos entre si? Vejamos um exemplo:

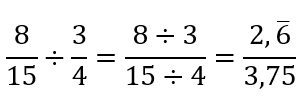
Ficamos com um resultado que causa estranheza, já que essa mistura de representação decimal, incluindo dízimas, não é usual nem prática. Mas a baixa conveniência da forma do resultado não necessariamente o torna incorreto. Vamos fazer um teste empírico, usando uma calculadora:

Se tivéssemos usado o algoritmo tradicional, chegaríamos – mais facilmente – ao resultado 32/45, cujo valor aproximado é 0,71111. Ou seja, mesmo nesse caso, parece que o algoritmo de Rafael é válido, embora não se mostre prático.

Mas, se realmente quisermos garantir de forma mais rigorosa a validade do algoritmo, teremos de recorrer a uma demonstração algébrica simples, na qual vamos tomar o algoritmo tradicional da divisão de frações como válido (o que já foi demonstrado no posto citado anteriormente).

Tomemos ainda duas frações genéricas representadas por a/b e c/d, com a inteiro e b, c e d inteiros não nulos.

Nesse ponto, podemos usar a propriedade comutativa e escrever:

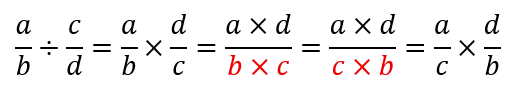
Porém, essa última expressão obtida é precisamente o resultado da divisão de a/c por b/d. Logo, usando uma simples troca notacional entre os símbolos de divisão e fração (operacionalmente equivalentes), temos o que queríamos provar:

Ou seja, embora nem sempre prático, é possível dividir frações por meio do algoritmo usado por Rafael: dividir numeradores e denominadores entre si. E, em alguns casos, esse pode até ser mais prático que o tradicional.

O importante aqui não é defender um ou outro algoritmo para divisão de frações que, aliás, não são os únicos possíveis (assunto para outro post!). Mas é demonstrar que a matemática não se equivale a um conjunto de regras procedimentais estanques. Existem muitos caminhos de pensamento diferentes, não apenas para resolver problemas, mas até mesmo para resolver operações numéricas fechadas. Ao olharmos para as ideias de nossos estudantes com atenção e curiosidade matemática, abrimos espaço para descobertas — e para nos lembrarmos de que a matemática é, antes de tudo, uma ciência viva, feita de raciocínios, conexões e diferentes formas de pensar.